Introduction
Modern spectrometers today, regardless of their size, employ sensitive linear CCD and CMOS sensors. The most popular sizes have 1024, 2048 and more recently 4096 pixels along the dispersion axis of the grating. Associated software automatically reads out a series of digitized values, each value corresponding to a single pixel element on the detector.

So once acquired, the spectral data are already in the form of signal intensity up the Y-axis and pixel value along the grating dispersion X-axis. It is usual, however, to convert the horizontal axis into the more meaningful units of wavelength (λ) and this becomes absolutely essential when spectral line identification of an unknown sample is the objective.
Wavelength Calibration
I will use the MS125 spectrometer as an example of the procedure. This spectrometer has interchangeable gratings and a micrometer screw to change the wavelength range. A fresh calibration must be performed when a grating is changed or the micrometer setting is adjusted. What we are doing with this procedure is mapping every pixel number on the linear array sensor to a specific wavelength and this is best performed with spectral calibration lamps that have very narrow emission lines whose wavelengths are known very precisely.

The relationship between pixel number and wavelength can be expressed as a third-order polynomial of general form
λp = I + C1p1 + C2p2 + C3p3
where λp is the wavelength of pixel number p, I is the wavelength of pixel number 0, and C1, C2 and C3 are first-order, second-order and third-order coefficients respectively in the polynomial expression. The objective is to determine values for I and the three coefficients.
The results of the calibration procedure are tabulated below:
Emission Line | True λ (nm) | Pixel # | (Pixel #)2 | (Pixel #)3 | Predicted λ (nm) | Residual |
|---|---|---|---|---|---|---|
Ar | 687.13 | 1003 | 1006009 | 1009027027 | 687.1479 | -0.01791 |
Ar | 675.28 | 962 | 925444 | 890277128 | 675.2666 | 0.013435 |
Ar | 667.73 | 936 | 876096 | 820025856 | 667.7032 | 0.026773 |
Ar | 641.63 | 847 | 717409 | 607645423 | 641.6432 | -0.01319 |
Hg | 579.07 | 637 | 405769 | 258474853 | 579.0997 | -0.02967 |
Hg | 576.96 | 630 | 396900 | 250047000 | 576.9892 | -0.02918 |
Hg | 546.07 | 528 | 278784 | 147197952 | 546.0464 | 0.023581 |
Hg | 491.60 | 351 | 123201 | 43243551 | 491.5016 | 0.098423 |
Hg | 435.84 | 174 | 30276 | 5268024 | 435.8645 | -0.02455 |
Hg | 433.36 | 166 | 27556 | 4574296 | 433.3238 | 0.036176 |
Ar | 430.01 | 156 | 24336 | 3796416 | 430.1447 | -0.13474 |
Ar | 426.63 | 145 | 21025 | 3048625 | 426.6436 | -0.01365 |
Ar | 425.94 | 143 | 20449 | 2924207 | 426.0066 | -0.06663 |
Ar | 419.95 | 124 | 15376 | 1906624 | 419.9478 | 0.00216 |
Ar | 415.86 | 111 | 12321 | 1367631 | 415.795 | 0.06503 |
Hg | 407.78 | 86 | 7396 | 636056 | 407.7918 | -0.01179 |
Hg | 404.66 | 76 | 5776 | 438976 | 404.5843 | 0.075715 |
A regression analysis is then performed on the above data with the following result in Figure 1:
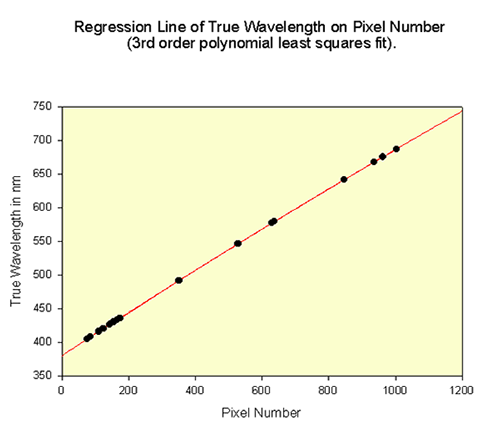
Evaluating the intercept and the three coefficients determine the relationship between actual wavelength and pixel number. The goodness of fit of the model should be very high, and the correlation coefficient (r2) should be a number very close to 1 (it is 0.9999997 in this example). An F test from an analysis of variance (ANOVA) should similarly produce a large number indicating a high degree of statistical significance. If r2 is not close to 1, this usually indicates that a wavelength value has been mistyped or incorrectly assigned during the procedure.
From the regression analysis, the relationship between the true wavelength and the pixel number in the measured spectra is given by the following expression:
True λ = 380.091 + 0.32365 (Pixel #) – 1.79 × 10-5(Pixel #)2 + 4.77 × 10–10(Pixel #)3
This equation only applies for a given grating and micrometer setting used in the experiment. Should these parameters change a new calibration procedure has to be performed. The calibration parameters (I, C1, C2, C3) are usually stored in a configuration file by the software that is unique to the grating and λ range used. Therefore once a calibration has been carried it does not need to be repeated (unless gratings are changed and/or the detector is moved as mentioned earlier).
Although at first glance it may look straight, the regression line above actually exhibits some slight curvature. A second order quadratic model may have been enough to fit the experimental data, but a 3rd order polynomial takes into account any sigmoidal variation in the data.
In general the dispersion of a grating is not exactly linear in wavelength and deviations from linearity can be both in a positive sense and a negative sense, leading to a very slight s-shaped form of the regression line. The extent of non-linear dispersion in gratings is primarily determined by the accuracy of the ruling engine used to physically rule the grooves on the grating during its manufacture. It is also limited by the machining tolerances of the micrometer wavelength drive in the spectrometer.
Small spectrographs such as the MS125 that employ micrometers to change the wavelength range usually use a sine-bar drive. This is a device built onto the support that holds the grating in the spectrometer. It usually consists of a bar with a hardened steel ball at the end which is in intimate contact with the polished flat end of the micrometer shaft. Small variations in the machining or alignment of the sine-bar drive will also contribute to the small deviations from linearity that are seen in the calibration curve.